ریاضیاتی سوچ : ٹرٹل بلاکس کے ساتھ کھیلتے ہوئے

ٹرٹل بلاکس ،ایک قسم کااوپن ڈیجیٹل کینوس (“اوپن” سے مراد مفت یا آزاد ڈیجیٹل مواد )ہے جسے خاص طور پر بچوں کے لیے بنایاگیا ہے۔ اس کے استعمال سے وہ کھیل کھیل میں ریاضی  کے تصورات کو دریافت یاان کی  بازیافت کر سکتے ہیں ۔ یہ ڈیجیٹل  کھیل کاایسا میدان مہیا کرتا ہےجہاں بچے فطری طور پر ریاضی سے جڑ سکتے ہیں۔اور شاید وہ اس قابل بھی بن جائیں  گے کہ جو ریاضی انہوں نے  اسکولی نصاب میں پڑھی ہے اس کو نہ صرف بہترطور پر سمجھ سکیں گے بلکہ اس کو پسند بھی کرنے لگیں گے۔ ٹرٹل بلاکس  دراصل “لوگو پروگرامنگ(logo programming)” کی طرز پر بنایا  گیا  ہے  جو MIT میڈیا لیاب میں 1960 کی دہائی میں بنائی گئی تھی۔

ٹرٹل بلاکس  تک رسائی مختلف آلات پر کی جا سکتی ہےجیسےکہ ڈیسک ٹاپ کمپیوٹر، لیپ ٹاپ، ٹیبلٹ اور اسمارٹ فونز۔لوگو پروگرامنگ کے بارے میں بات سیمور پیپرٹ (Seymour Papert)کے تذکر ےکے بغیر ادھوری رہے گی ، جن سے ہم سب “کمپیوٹیشنل سوچ(computational thinking)کی اصطلاح مستعار لیتے ہیں۔پیپرٹ نے جین پیاجے ( Jean Piaget) کے ساتھ کام کرتے ہوئے تعمیراتی نظریہ (constructionism)کی بناءڈالی    جس کی بنیاد”بنا کر سیکھنے” پر مبنی ہے۔، اس نظریہ کو وجود میں لانے  کے لئے انہوں نے جین پیاجےکے (constructivism)  کا سہارا لیا جو اس اصول کو بنیاد بناتا ہے کہ سیکھنے والے فعال طور پرخود اپنی سمجھ کو ترتیب دیتے ہیں۔

[1] (Ackerman)کے مطابق، تعمیراتی نظریہ کا زور‘ہاتھوں سے مشق کرتے ہوئے سیکھنے‘ پر ہے اوروہ اس امر کی تشریح میں ہماری مدد کرتا ہےکہ”نظریات کس طرح بنتے ہیں اور تبدیل ہوتے ہیں جب انھیں مختلف میڈیا کے واسطے سے اظہار کیا جاتا ہے،مخصوص  سیاق میں جب ان کو برتا جاتا ہے  اور جب ہر فرد ان پر انفرادی طور پراپنا سر دھنتاہے  “۔

ایم آئی ٹی میڈیا لیب میں، پیپر ٹ نے لوگو پروگرامنگ کی تخلیق ایک جسمانی روبوٹ  کے ذریعہ کی  جس کی حرکت کو ہدایات کے پابند کیا جا سکتا ہے۔انہوں نے بچوں کے لئے کھلے اور آزاد  موقع و محل کا خواب دیکھا تھا جس میں وہ ریاضی برت سکیں اور اس کو انہوں نے [3] ( mathland) سے موسوم کیا۔

(Mathland)، درحقیقت ، کوئی بھی جگہ ہو سکتی ہےجو ضروری نہیں کہ ہمیشہ ورچوئل (virtual)ہی ہو، جہاں سیکھنے والے،  اشیاء کے ساتھ کھیل سکتے ہیں اور قدرتی ماحول میں ریاضی کا تجربہ کرسکیں۔ تاہم ڈیجیٹل واسطہ در اصل بہت سے امکانات فراہم کرتا ہے جو محدود اینالاگ  واسطے(analog medium) میں مشکل سے فراہم کیا جاسکتا  ہے۔

لہذاٹرٹل اور لوگو پروگرامنگ کو ڈیجیٹل شکل میں نقل (simulate) کیا گیا تھا جو  اب ٹرٹل پروگرامنگ سافٹ وئیر [5]کی شکل میں موجود ہے۔اس سافٹ ویئر میں، مجازی (virtual)پروگرامنگ بلاکس (blocks) ہوتے ہیں جس طرح طبیعی دنیا (tangible mode) میں  لیگو (lego)کےبلاکس ہوتے ہیں  جنہیں آپس میں ترتیب دے کر ہدایت کی شکل دی جاسکتی ہے اور کمپیوٹر کے پردے پر ایک کچھوے جیسے مجازی جانور کو جیسے چاہے ویسے حرکت  دی جاسکتی ہے۔لہذاصارف (user)اگر چاہے کہ کچھوے کو سیدھی لکیرپر چلائےیا دائرے کی شکل میں  گھمائے ، پروگرامنگ کے بلاکس کا استعمال کرتے ہوئے بآسانی یہ کام کیا جاسکتا  ہے۔ کچھوا صارف  کی  ہدایات کے مطابق مخصوص رنگ  کی پیروی کرتے ہوئے اپنے راستے پرحرکت کرتا رہتاہے ۔اس طریقے سے مناسب ہدایات دے کر بہت سی شکلیں اور خاکے (patterns) بنائے جاسکتے ہیں۔ مخصوص  خواص کی حامل شکلیں بنانے کے لئے ہدایات بیان کرنے کا عمل  بذات خود ریاضیاتی سوچ کو پروان چڑھاتا ہے۔

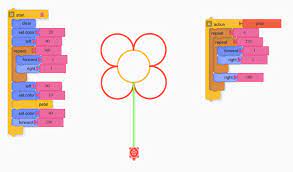
شکل1  : چاراہم پروگرامنگ بلاکس کی وضاحت کرتی ہے۔

شکل 1چار اہم  پروگرامنگ بلاکس  کی وضاحت کرتی ہے جوکچھوے کو ایک مخصوص سمت میں حرکت کرنے پر مجبور کرتےہیں۔

ہر بلاکس  کے ساتھ ایک عددمنسلک ہوتا ہے جواس بلاک کی  نقل و حرکت (سمت اورفاصلے)کا منتظم ہوتا ہے۔Forward اور backward کمانڈس،کچھوے کوسیدھی لکیر میں حرکت دینے میں مدد دیتے ہیں۔ ( 100 forward) کا مطلب یہ ہے کہ کچھوا   100 قدم آگے بڑھے گا اور (backward 100 )کا مطلب یہ ہے کہ کچھوا   100 قدم پیچھے کی جانب بڑھے گا ۔اسی طرح right اور left والے کمانڈس کچھوے کو دائیں اور بائیں جانب  گھماتے ہیں، لہذا right 90کا مطلب یہ ہے کہ دائیں جانب 90 ڈگری تک گھومے گا اور left 90 کا مطلب یہ ہے کہ بائیں جانب 90 ڈگری تک گھومے گا۔

ریاضیاتی سوچ کیوں اہم ہے؟

آئیے ان پروگرامنگ بلاکس  کو استعمال کرتے ہوئے ایک مستطیل  بناتے ہیں۔سب سے پہلے ہم کچھوے کو سیدھی لکیر پرمخصوص فاصلے(100 قدم)چلنے کے لئے ہدایت دیں گے۔اب  90 ڈگری دائیں جانب گھمائیے۔اس کے بعد کچھوے کو آگے کی جانب سیدھی لکیر پر 50 قدم کے فاصلےتک بڑھائیں،اور پھر اسے دائیں جانب موڑ دیں یہاں تک  کہ کچھوا اپنے ابتدائی نقطے پر پہونچ جائے۔اس نہج پر مختلف اشکال  بناکر ان کی ریاضیاتی خصوصیات کا تجربہ کیا جاسکتا ہے۔

شکل3: ایک مستطیل بنانے کے لئے ٹرٹل بلاکس کوہدایات ۔

ٹرٹل بلاکس کوتدریسی نقطہ نظر سے بھی استعمال کیا جاسکتا ہے۔مجھےاس ڈیجیٹل آلے (tool)کے فوائد اور استعمالات کو دریافت کرنے کا اس وقت موقع ملا جب میں نے اپنی آٹھ سالہ بیٹی کو اس سے متعارف کروایا۔درحقیقت، ٹرٹل بلاکس کو کم عمر بچوں میں بھی متعارف کروایا جا سکتا ہے۔ میری بیٹی کچھوے کو اپنی دی گئی ہدایات پر عمل کرتے ہوئے دیکھ کر بہت محظوظ ہوئی۔

شکل 4: ٹرٹل بلاکس کا استعمال کرتے ہوئے پیچیدہ خاکے(patterns)بنائے گئے ہیں۔

پروگرامنگ کرتے ہوئے کچھوے کواپنے من پسندانداز میں ترتیب (design)کرنے کے بعد اس کواپنے اختیار(control) کا احساس ہوااوراس کے تخیل کو جلا بھی ملی جس سے وہ مزید اشکال اورخاکے(patterns) بناسکی۔ مزید برآں اس کو اشکال اورخاکوں کو ریاضیاتی انداز میں سوچنے کا داعیہ بھی ملا۔

اوپن (آزاد)ڈیجیٹل کینوس یا کھیل کا میدان

اکثر ڈیجیٹل گیمز اور پلیٹ فارمز کے برعکس، ٹرٹل بلاکس ایک کورے کاغذ کی طرح ہے جہاں بچےاپنےتخیل کو کام میں لا سکتےہیں۔ وہ یہ فیصلہ کر سکتےہیں کہ  شکل یا  خاکے کی تخلیق کس طرز پرہو اور پھر خود اپنی ریاضیاتی سوچ کو استعمال کرمطلوبہ شکل  کو بنانے کے لئےپروگرامنگ کرسکتے ہیں۔ یہ آلہ (tool)اس معنی میں آزاد ہے کہ یہ  ایک ایسا میدان  اور اشیاء فراہم کرتا ہے جس میں بچے   کھیل سکتے ہیں۔جو دراصل بچوں کو بنی بنائی اشیاء کے ساتھ غیر فعال طریقے سے کھیل میں مگن نہیں کرتا بلکہ انہیں اس قابل بناتا ہے کہ وہ اشیاء کے ساتھ اپنے تخیل  کو بروئے کار لائیں۔

آلے کے ساتھ کھیل کے ابتدائی مرحلے سے گزرنےکے بعد،بچے خود اپنےچیلنجس  تیار کریں  گے اورخودنئے مسائل کی نشاندہی کریں گے۔یہ تجربہ نہ صرف مزے دار ہوتا ہے بلکہ فائدہ مند بھی ہوتا ہے۔البتہ ابتداء میں اس آلے کے استعمال  کے لئے ابھارنے اورسہارے کی ضرورت ہوگی۔

کھیل کھیل میں مسائل کا حل

ٹرٹل کے بلاکس  کے ساتھ کھیلتے ہوئے بچے پہلے تو آسان اشکال کی تخلیق کریں گے لیکن آہستہ آہستہ وہ  پیچیدہ  اشکال اور خاکوں کو بنانے کی کوشش کرنے لگیں گے۔شکل6 میں چند ایسے ہی پیچیدہ خاکوں کی مثالیں دی گئی ہیں۔

شکل5 :لانچ ہونے پر ٹرٹل بلاکس ایک کھلا کینوس دکھاتا ہے

شکل 6: ٹرٹل بلاکس کا استعمال کرتے ہوئے بنائے گئے خاکوں کی مثالیں۔

یہ سافٹ ویئر تیار شدہ مسائل فراہم نہیں کرتا ۔ تاہم، یہ اس امر کی حوصلہ افزائی کرتا ہے کہ صارف (user)آسان اشکال کو سیکھ کر نئے خاکوں(pattern)کے بارے میں سوچنےلگے۔ پیچیدہ نمونوں کو بنانےکے لئے، جیسا کہ شکل6 میں واضح کیا گیا ہے، صارف کو نئے سرے سے ہدایات تخلیق کرنا ہوگا ۔ بالترتیب اور مستقل کوشش اورغلطی   کا طریقہ اپنایا جاتا ہےجس میں ہدایات کو بہتر سے بہتر کیا جاتاہےتا آنکہ مطلوبہ خاکہ حاصل ہوجائے۔ مخصوص شکل  کی تخلیق کرنے کے قابل ہونے  پر بچوں کو کامیابی کا احساس ہوتا ہے۔میں نے اپنی بیٹی کے  معاملےمیں یہ مشاہدہ کیا ہے کہ وہ دھیرے دھیرے سادہ شکلوں سے آگے بڑھتے ہوئے مزید دلچسپ اور پیچیدہ شکلیں بنانےلگی ۔

 شکل7میں ایک مثال  دی گئی ہے جس میں اس نے پہلی بار ایک دائرےکو بنایا پھرکوڈ(code) کا استعمال کرتے ہوئےایک دوسرے کو ملنے والے دا‏ئروں  کو بنایا۔شکل 7 میں یہ بتلایا گیا ہے کہ کس طرح دائروں کو دہراکر ایک خاکہ (pattern) تخلیق کیا گیا۔ہر دائرے میں 4 رنگ ہیں  کیوں کہ محیط کے چاروں ربعوں کا رنگ الگ الگ ہے۔چونکہ اس خاکے  میں 5 دائرے ہیں اس لئے ماڈیول (module) کواصل پروگرام میں 5 بار دہرایا گیا۔اس ماڈیول میں 4 رنگوں کو استعمال کرتے ہوئے دائرے کو  بنانے کے لئے ہدایات موجودہیں۔اس میں کچھوے کو دائرے کے ایک چوتھائی حصے کو عبور کرنے کے لئے لال رنگ استعمال کرنے کی ہدایت دی گئی  ہے،اس کے بعد ایک چوتھائی حصے کے  لئے نیلا   وغیرہ۔ان تمام مرحلوں کے بعد آپ دیکھ سکتے ہیں کہ چار مختلف رنگوں  سے لیس ایک دائرہ وجود میں آتا ہے۔جیسے ہی پہلا دائرہ بن جاتاہےکچھوے کو نئے دائرے کے نقطہ آغاز پر رکھ کرماڈیول کو پھر 5 بار دہرایا جاتا ہے۔اسی طرح اس عمل کو بھی  5 باردہرا کر ایک دوسرے میں ملے ہوئے دائروں کا ایک خوب صورت خاکہ ہمارے سامنے نمودارہوتا ہے۔

شکل 7: ٹرٹل بلاکس کا استعمال کرتے ہوئے دائروں کو آپس میں ملانے کا ایک خاکہ۔

قدرتی ماحول میں تصورات کی سمجھ

ٹرٹل کے بلاکس کے ذریعہ دائرے کو بنانے سے بچوں میں وجدانی انداز میں یہ بات سمجھ میں آجائے گی کہ ‘ڈگری’کو زاویہ کی پیما‏ئش کے لئے استعمال کیا جاتا ہے ۔ یہی میری بیٹی کے ساتھ بھی ہوا۔ اس نے اس حقیقت  کا  ادراک کیا کہ کچھوے کو کتنا گھمایا جائے اس بات کا صحیح اندازہ   ڈگری سے لگایا جاسکتا ہے ۔اس طرح سے زاویہ اور اس کی پیمائش سے متعلق اس کی سمجھ   پختہ ہو‏ئی قبل  اس کے کہ یہی تصورات وہ اسکول میں پڑھے۔

خود سے الگورتھم کی  تخلیق

ٹرٹل بلاکس بچوں کو اس بات پر ابھارتا ہے کہ وہ اپنے آپ کو چیلنج کریں۔مزید برآں کسی مسئلہ کا  حل کئی طریقوں سے نکالا جاسکتا ہے جو ایک ریاضی کلاس روم کے اس عمومی طریقے سے قدرے مختلف ہےجومسلسل مشق  سے عبارت ہوتا ہے۔ جب کبھی طالب علم کو کو‏ئی مسئلہ درپیش ہو تو اس پر لازم  ہے کہ مسئلہ کا حل خود دریافت کرنے کے لئے خود سے الگورتھم بنائے۔اکثر”مسلسل کوشش اورغلطی(trial and error)مثالوں  کی مدد سے سیکھنا(building from examples) اور مسئلہ کو چھوٹے چھوٹے  آسان مسائل میں تقسیم کرنا(breaking a problem into) (simpler problems)جیسی حکمت عملیاں عمل میں لائی جاسکتی ہیں۔شکل8 میں یہ بتلایا گیا ہے کہ کیسے ایک معمول سے ہٹ کراور پیچیدہ خاکہ سب روٹین (subroutine)کو دہراکر وجود میں لایا گیا۔

 مسئلہ کو چھوٹے چھوٹے  آسان مسائل میں تقسیم کرنا

کسی مسئلہ کو چھوٹے چھوٹے  آسان مسائل میں تقسیم کرتے ہوئے اس کا حل نکالنا ایک اہم اور مشہور حکمت عملی ہے۔میں نے میری بیٹی کو بھی اسے بروئے کار لاتے ہوئے دیکھا۔اشکال 7 اور 9 میں دی گئی مثالوں میں ہم نے دیکھا کہ بڑے مسئلے میں چھوٹی سب روٹین (subroutine) پائی جاتی ہیں۔

ایک پیچیدہ خاکہ درحقیقت چھوٹے آسان خاکوں پر مشتمل ہوتا ہے جنہیں سب روٹین (subroutine) کی شکل میں کوڈ (code) کیا جاسکتا ہے۔

شکل8: مرکزی پروگرام (main program)میں سب روٹین کو شامل کرکے بنایا گیا ایک خاکہ۔

ایک طریقہ یہ ہے کہ سب روٹینس (subroutines) کو آسان مسائل کے لئے لکھا جائے اور انہیں ملاکر بڑا مرکزی پروگرام بنایا جائے۔

غلطیوں سے سیکھنا

بچے ٹرٹل بلاکس کے ساتھ کھیلتے وقت جب غلطیاں کرتے ہیں توانہیں مزید یہ سوچنے کا موقع ملتاہے کہ مطلوبہ خاکے کو حاصل کرنے کا طریقہ  کیا ہے۔ہر بار جب بچہ مطلوبہ شکل نہیں اتار سکتا ، اس کو واپس جاکر اپنے الگورتھم کو ٹھیک کرنا ہوتا ہے۔لہذا غلطیوں کو سدھارنا بھی بذات خود دلچسپ چیلنج سے کم نہیں ہوتا۔

شکل 9 کے خاکےمیں یہ دکھلایا گیا ہے کہ ایک ہم آہنگ خاکے(symmetrical pattern) کو بنانے میں” مسلسل کوشش اورغلطی ” والا طریقہ کیسے ممد و معاون  ثابت ہوتا ہے۔

اس شکل کے ماڈیول نمبر ایک میں دل کو اتارنے کی ہدایات موجود ہیں۔میری بیٹی نے اس ماڈیول کے ذریعہ ایک دوسرے پر منطبق دلوں کو اتارنے کی کوشش کی۔ابتداءمیں اس نے ماڈیول نمبر ایک کو 5 بار دہرایا(called 5 times) اور گھومنے کا زاویہ 63 ڈگری چنا۔لیکن  نتیجہ ایک غیر “ہم آہنگ “خاکے کی صورت میں سامنے آیا۔یہاں یہ واضح رہے کہ مرکزی پروگرام ، دل کو اتارنے والے ماڈیول کو کئی بار دہراتا ہے اور ہر بار دل مختلف زاویےکے ساتھ گھومتا ہے۔دوسری بار اس نے زاویے کو 69 ڈگری چنا لیکن اس بار بھی مطلوبہ نتیجہ نہیں  پاسکی۔بالآخر 72 ڈگری چننے پر ایک بہترین ہم آہنگ خاکہ وجود میں آیا جو شکل 9 کے بالکل دائیں جانب دیکھا جاسکتا ہے۔اس یوریکا لمحے (eureka moment) نے اس مباحثے کو آگے بڑھایا  کہ 72 ڈگری   چننے پر ہی  کیوں مطلوبہ ہم آہنگ خاکہ وجود میں آیا۔کیسے کوئی یہ نتیجہ اخذ کرسکتا ہے کہ 72 ڈگری ہی وہ زاویہ   ہے جو مطلوبہ خاکہ بناسکتا ہے۔

کچھ مدد کے بعد وہ اس قیاس تک پہونچی کہ 360 ڈگری  کو 5 سے تقسیم کرنے پر 72 ڈگری ہوتا ہے۔لہذا گھومنے کا زاویہ 72 ڈگری لینے  پر دلوں کی محتلف تصاویر ہم آہنگ انداز میں ترتیب پاتی ہیں۔

تصاویر اور خاکوں میں موجود ریاضیاتی تصورات  سے واقفیت اور ا ن کی اہمیت  کا اندازہ

چھوٹے بچے جب ٹرٹل بلاکس کے ساتھ کھیلتے ہیں تو خاکوں میں  موجود کارفرما ریاضی سے واقفیت انہیں قدرتی طور پر ہوجاتی ہے۔وہ ان تصورات کو روزمرہ زندگی میں بھی لے جاتے ہیں۔ میں نے اس امر  کا مشاہدہ کیا کہ میری بیٹی اپنے اطراف مختلف قدرتی خاکوں کو دیکھ کر ٹرٹل بلا کس میں انہیں کوڈ(code) کرنے کی کوشش کرتی ہے۔

 ہم نے   خاکوں کو بنانے کے کئی دیگر طریقوں پر بھی سیر حاصل بحث کی   اور ان  میں کارفرماریاضی  کو سمجھنے کی کوشش کی۔ریاضی کو سمجھنے کے طریقوں میں ایک اہم طریقہ خاکوں کا مشاہدہ کرنا ہے،نہ صرف جیومٹری میں بلکہ اعداد اور ان کے نمائندہ تصورات جیسےالجبرا، علم مثلث (trigonometry) اوراسکولی نصاب میں موجود دیگر کئی دوسرے تصورات میں بھی خاکوں کا مشاہدہ بھی اس میں مدد دیتا ہے۔ٹرٹل بلاکس چھوٹے بچوں میں جیومٹری کے خاکوں کو لے کر تجسس پیدا کرتا ہے ۔

ایک ہی مسئلہ کو حل کرنے کے کئی طریقے

ٹرٹل بلاکس کو استعمال والا اپنے آپ کو یہ چیلنج دے سکتا ہے کہ ایک ہی مسئلہ کو مختلف طریقوں سے حل کرے۔کبھی کبھار ایسا ہوتا ہے کہ ایک خاص طریقےسےمسئلے کو حل کرنے سے مراحل کی تعداد میں کمی آتی  ہے۔مثال کے طور پر ایک مستطیل بناتے وقت آپ نے مشاہدہ کیا ہوگا کہ چند سلسلہ وارمرحلوں کو دہرانا پڑتا ہے۔اس قسم کے مراحل کو مرکزی پروگرام کے کوڈ میں لوپ(loop) کی مدد سے ترتیب دیا جا سکتا ہے۔لوپس (loops) پروگرام کو تبدیل کرنے میں مدد دیتے ہیں تا کہ صارف مختلف طریقے اپناتے ہوئے اپنے مطلوبہ حل تک پہونچ سکے۔کوڈ کو تبدیل کرتے ہوئے اس  میں نکھار پیدا کرنے کا عمل اپنے آپ میں خودایک بہترین سیکھنے کا طریقہ ہے۔میں نے کئی بار یہ دیکھا ہے کہ میری بیٹی اپنے لکھے ہوئے کوڈ کو بہت طمانیت  کے ساتھ بیان کرتی ہے اور خود اس میں تبدیلی کرتے ہوئے کچھ دیگر ہدایات  کو ترتیب دینے لگتی ہے۔

شکل 10: دائروں سے خاکے  کیسے نکلتے ہیں۔

شکل 11: ٹرٹل بلاکس کا استعمال کرتے ہوئے حاصل کردہ ایک ہم آہنگ خاکہ۔

ٹرٹل بلاکس  آلے (tool)کی جانب سے فراہم کردہ  یہ موقع  صارف  کی توجہ کو مسئلے کے حل کے  مختلف طریقوں  کے تئیں ابھارتا ہے۔

ہم آہنگیت کی بازیافت

ٹرٹل بلاکس کے استعمال کے دوران کئی ایسی شکلیں اور خاکے وجود میں آئیں گے جو ہم آہنگ(symmetric) ہوں گے۔میں نے مشاہدہ کیا کہ جب بھی میری بیٹی کوئی خاکہ بناتی ہے اس میں  کسی نہ کسی شکل میں ہم آہنگیت  موجود ہوتی ہے۔اگر کبھی ہم آہنگیت نہیں پائی جاتی تو وہ فوری اپنی دی گئی ہدایات کو بدلتی ہے یہاں تک کہ خاکے میں ہم آہنگیت  دکھنے لگے۔شکل 11 میں ایک ایسے ہم آہنگ خاکے کی مثال دی گئی ہے جو آزادانہ کوشش سے وجود میں آیا تھا۔

کیا ٹرٹل بلاکس کوڈنگ کے متعلق آلہ ہے؟

کوڈنگ(coding) آج کل زبان زد خاص و عام چیز ہے اور ٹرٹل بلاکس کو دیکھ کر ایسا محسوس بھی ہوسکتا ہے کہ یہ ایک اور سافٹ وئیر پروگرام ہے جو پروگرامنگ سیکھنے میں مدد کرتا ہے۔درآں حالیکہ یہ آلہ پروگرامنگ سےکچھ شد بد رکھتا ہے لیکن  اس کی نوعیت  ان تمام تجارتی نوعیت کے آلوں (commercial tools) سے قدرےالگ ہے جوبچوں کو پروگرامنگ  کی تکنیکوں سےواقف کرواتے ہیں۔یہ بچوں کو وجدان کی سطح پر خاکوں کی سمجھ  عطا کرتا ہے اور انہیں مسئلے کے حل میں مشغول کرتاہے۔یہ ایسی صلاحیتیں بچوں میں ودیعت کرتا ہے جوانہیں نئے خاکوں کو بنانے کےلئے اورمسئلوں کو حل کرنے کے لئے کوڈ لکھنے میں مدد کرتے ہیں۔بلکہ یہ کہنا بعید از حقیقت نہیں ہے کہ یہ آلہ بچوں میں کمپیوٹیشنل سوچ (computational thinking)پیدکرتا ہےجس میں( decomposition)، تجرید (abstraction)، الگورتھم کی تخلیق اور کوڈ کی تفتیش شامل ہیں۔

جینیٹ ونگ کے مطابق [4]:

” کمپیوٹیشنل سوچ (computational thinking) نہ صرف کمپیوٹر کے سائنس داں بلکہ ہر کسی کے لئے ایک  بنیادی صلاحیت ہے۔لکھنے، پڑھنے اور حساب دانی کے ساتھ ساتھ ہمیں کمپیوٹیشنل سوچ کو بھی ہر بچے کی  تجزیاتی صلاحیتوں میں گننا چاہئے۔ “

ونگ [2،4] مزید یہ استدلال کرتی  ہیں کہ کمپیوٹیشنل سوچ دراصل ایک کمپیوٹر سائنس داں کی طرح سوچنے سےعبارت ہے “جس کا مطلب کمپیوٹر کو پروگرام کرنے (ہدایت دینے) سے کہیں بڑھ کر ہے۔یہ کئی سطحوں پر تجریدی سوچ کا مطالبہ کرتا ہے۔”لہذا کمپیوٹیشنل سوچ  محض کوڈ لکھنے کا نام نہیں ہے بلکہ درحقیقت  یہ ادراک کہ مشینوں سے کیسے بات چیت کی جائے تاکہ آپ اس سے کام لے سکیں    اور اسی طرز پر  سوچتے ہوئے مسئلے کے حل کے لئے کمپیوٹر کا بہتر استعمال کیسے کیا جاسکتا ہے۔

ٹرٹل بلاکس بچوں میں کمپیوٹیشنل سوچ  پیدا کرنے اور اس کی نشونما دینے میں ایک اہم آلہ ثابت ہوسکتا ہے۔یہ آلہ اوپن (اپنی فطرت میں وسعت رکھتا ہے)اور بہیترے ممکنات کا میدان اپنے اندر رکھتا ہے۔یہ ایسا ہی ہےجیسا  کہ ایک  بچے کو کینوس (canvas) اور پینٹ برش (paintbrush) دے دیا جائے۔ 21 ویں صدی میں، کسی کمپیوٹنگ مشین کو پروگرام کرنے کی صلاحیت ایک اہم بنیادی صلاحیت مانی جاتی ہے۔ٹرٹل بلاکس جیسا آلہ کمپیوٹیشنل سوچ میں مشغول کرنے کے لئے بہترین قدرتی ماحول مہیا کرتا ہے۔

 

ویب سائٹس اور ایپس جہاں سے ٹرٹل بلاکس   تک رسائی کی جاسکتی ہے:

https://turtle.sugarlabs.org/
2.  https://apps.apple.com/us/app/turtles-learn-to-code-for-fun/id1454902715
3. Javascript/HTML5 port of Turtle Blocks: https://github.com/sugarlabs/turtleblocksjs
4. https://blockly.games/turtle?lang=en

حوالہ جات:

[1] Ackermann, Edith K. (2004): Constructing Knowledge And Transforming The world, A learning zone of one’s own: Sharing
representations and flow in collaborative learning environments [M. Tokoro and L.Steels (Eds.). Amsterdam, Berlin, Oxford, Tokyo,
Washington, DC. IOS Press, 2004. Part 1. Chapt 2. pp. 15-37.
[2] Cuny, J., Snyder, L., & Wing, J.M. (2010): Demystifying computational thinking for noncomputer scientists. Unpublished
manuscript in progress, referenced in http://www.cs.cmu.edu/~CompThink/resources/TheLinkWing.pdf

 [3] Papert, S. (1980): Mindstorms. Children, Computers and Powerful Ideas. New York: Basic books.
[4] Wing J.M. (2006): Computational thinking. Communications of the ACM, 49(3), 33-35.
[5] https://el.media.mit.edu/logo-foundation/what_is_logo/history.html

 

بشکریہ: 

At Right Angles (A Resource for School Mathematics) – Issue 11| Nov 2021 

مضمون نگار: مجاہد الاسلام  (ایجوکیشن ٹکنالوجی کے ماہر،  [email protected])، عظیم پریمجی یونیورسٹی، بنگلور

مترجم :   عبدالمؤمن