مصنف: شئیلیش شرالی
ہندسہ کا تصور ریاضی کیلئے نہایت اہم ہے، تاہم اسکی ابتداء ہم سے ہمیشہ پوشیدہ رہے گی، کیونکہ یہ قدیم ترین دور سے وابستہ ہے۔ انسانوں نے بہت پہلے ہی تجارتی کھاتوں کے حساب کیلئے اعداد و شمار کا نظام اختیار کیا ہوگا بس ہم یہ نہیں کہہ سکتے کہ کب؟ 1960 میں ایشانگو بون کے بیلجین کونگو میں کی گئی ایک گراں قدر دریافت جو کہ 20000 سال بی پی قبل کی ہے یہ بتاتی ہیکہ ریاضی کی سوچ کے بیج ہمارے اندازوں سے بھی پچھلے ادوار میں ہو سکتے ہیں؛ ہڈیوں پر بنے ہوئے نقش توازن کی طرح ہیں جنہیں ایک دانستہ ترتیب میں لکھا گیا ہے جو ایک ریاضی کے خاکے کی طرف اشارہ کرتے ہیں [اس میں دوگنی ترتیب کا اشارہ بھی ہے: ۲،۴،۸۔۔۔۔]۔پھر بھی مزید شہادت ملنے تک اسے ایک قیاس ہی مانا جائیگا۔ مکمل جانکاری کیلئے ویکیپیڈیا کے حوالے دیکھئے۔

توازن (tally) کی گنتی کا عمل کم و بیش ۵۰۰۰۰ سال قدیم ہے۔ آج بھی ہم اسکو گنتی کیلئے مختلف پس منظر میں استعمال کرتے ہیں، مثلاً کلاس کے انتخاب میں۔
اعداد کا اعشاری نظام
جو علامات ہم آج استعمال کرتے ہیں – اعشاری نظام کی ابتداء قدیم زمانے میں ہوئی ہے۔ بہت پہلے اہل بابل {بابلین} نے ایک نظام استعمال کیا جو 60 کی قوت پرمبنی تھا اور اس نظام کے نقوش آج بھی موجود ہیں جیسے ایک منٹ میں60 سکینڈ، ایک گھنٹہ میں 60 منٹ اور ایک ڈگری میں 60 منٹ[زاویائی پیمائش میں]۔ آگے چل کر اہل مصر نے 10 کی قوت پر مبنی ایک نظام مرتب کیا جس میں ہر 10 کی قوت ، 10 سے 10 لاکھ تک ایک منفرد علامت سےظاہر کی جاتی تھی ۔ لیکن یہ نظام موجودہ نظام سے قطعی مختلف تھا کیونکہ اس میں صفر کی علامت کا فقدان تھا۔
صفر کی علامت کے بغیر علم ہندسہ کا نظام دو طرح کی مشکلات سے دوچار ہوتا ہے۔ اول یہ کہ بعض اعداد میں ہمیشہ الجھن رہتی ہے۔ مثلاً 23 جو 2 دہائی اور 3 اکائی کی نمائندگی کرتا ہےاور 203 جو 2 سیکڑہ اور 3 دہائی کی نمائندگی کرتا ہے۔ صفر کی علامت کے بغیر کوئی تو تدبیر چاہئے تھی جو بتاتی کہ2 یعنی 2 سیکڑہ ہے نہ کہ 2 دہائی۔ یہ کیا جا سکتا ہے لیکن بار گراں ہے۔ اس سے بھی بڑی مشکل یہ کہ حساب کرنا مشکل ترہوجائیگا اور علم ہندسہ میں ترقی بھی بہت مشکل ہوگی۔
اہل یونان کے پاس صفر کیلئے کوئی علامت نہیں تھی اور یہ قابل تعجب نہیں ہے کہ انہوں نے علم ہندسہ اور الجبراءمیں اسطرح ترقی نہیں کی جسطرح انہوں نے جیومیٹری کو نشونما دی اور بہت آگے بڑھایا۔ وہ سرزمین ہندوستان تھی جہاں{پانچویں صدی کے اوائل میں} صفر کی علامت کا وجود ہوا اسکے استعمال کے قواعد و ضوابط کے ساتھ۔ یہ اتفاق نہیں ہے کہ آریہ بھٹا، برہمہ گپتہ، مہاویر، بھاسکرآچاریہ دوم، اور کئی دیگر دانشوروں کے ہاتھوں علم ہندسہ اور الجبراءنے ہندوستان میں متاثرکن انداز میں ترقی کی۔
دوسری جانب قدیم اہل ہند نے جیومیٹری میں کوئی قابل قدر پیشقدمی نہیں کی۔ لیکن یہ بات قابل ذکر ہیکہ ایک حصہ جہاں الجبراء اور تجزیہ کے طریقے قدرتی انداز میں جیومیٹری میں داخل ہوتےہیں بنام ‘علم مثلثات'[ٹرگنومیٹری]، ہندوستان میں وجود پذیر ہوا {پانچویں صدی عیسوی، آریہ بھٹا کی تصنیفات}۔
تجرید (Abstraction) اور ہندسہ کا تصور
ہمارے ذہن میں ایک غیر معمولی صلاحیت موجود ہے: تصور کرنے کی صلاحیت، چیزوں اور مظاہر سے خصوصیات اور مشترکہ خوبیوں کو کشید کرنے کی صلاحیت۔ یہی صلاحیت زبانوں کی ترویج کے پیچھے کارگر ہے اور اسی نے ہندسوں کی ایجاد کے قابل بنایا ہے۔ اس بات کو سمجھنے کیلئے ایک ہندسہ 3 تصور کیجئے، کیا 3 کوئی شئے ہے؟ کیا یہ کہیں واقع ہو سکتا ہے؟ نہیں ایسا نہیں ہو سکتا۔ لیکن ہمارے ذہن میں اشیا ء کے مجموعے میں 3 ہونے کی خوبی کو دیکھنے کی صلاحیت موجود ہے۔ تین انگلیاں ، تین پرندے، تین بلی کے بچے، تین کتے کے بچے، تین لوگ وغیرہ۔ جو وصف ان میں مشترک ہے وہ تین ہونے کی خوبی ہے۔ یہ صلاحیت ہماری ذہنی ساخت میں جبلی طور پر موجود ہے، اوراگر ایسا نہیں ہوتا تو ہم کبھی بھی اعداد کے تصور کو جان نہیں پاتے{یا کسی اور اسطرح کے تصور کو، کیونکہ ہر تصور لازماً ایک تجرید ہے}
میزانی گنتی جیسے آسان کاموں میں – اشیاء کے مجموعہ اور میزانی نشانات کے مجموعہ میں ۱-۱ مطابقت پیدا کرنے میں ہمارا ذہن تجرید کی ایزدی صلاحیت کا مظاہرہ کرتا ہے، اور دانستہ طور پر مختلف اشیاء کی تفصیلات کو نظر انداز کرتے ہوئے انہیں گمنام وجود تصور کرتا ہے۔
اس گہری بصیرت کے شعور کے نتائج فن تعلیم پر ہوتے ہیں؛ جیسے، بڑا حکیمانہ قول ہیکہ ” تصورات سکھائے نہیں جاتے بلکہ اخذ کئے جاتے ہیں”۔ کسی کے ذہن میں تخیلات اور تصورات اشیاء کے مجموعہ کے ساتھ حقیقی تعلق سے ہی تخلیق پاتے ہیں۔ یہ کسطرح ہوتا ہے اسے ابھی مکمل سمجھا نہیں جا سکا ہے لیکن مجھے ایک تبصرہ یاد آتا ہے جوسقراط سے منسوب ہے{ استاد کا کردار ایک دائی کی طرح ہے جو بچے کی پیدائش میں مدد کرتی ہے}۔
الجبراء کی ایجاد تجرید کی سیڑھی پر ایک اور زینہ بڑھنے کو ظاہر کرتا ہے۔ اسکی تشریح کیلئے آئیے ہم ان ہندسی حقائق پر غور کرتے ہیں: 1+3= 4، 3+5=8، 5+7=12، 7+9=16، 9+11=20۔ ہمیں ایک واضح خاکہ نظر آتا ہے: دو متواتر طاق اعداد کا مجموعہ ہمیشہ 4 کا حاصل ضرب ہوتا ہے۔ اس بیان کی تصدیق ممکنات کی فہرست مرتب کرنے سے نہیں کی جا سکتی، کیونکہ وہ بہت زیادہ بلکہ لامتناہی ہیں۔لیکن ہم الجبرائی طریقے استعمال کر سکتے ہیں، ہمیں ان مشاہدات کو صرف الجبرائی بیان میں تبدیل کرنا ہے۔ 2n-1)+(2n+1)=4n) یہ فوراً اس بیان کو ثابت کرتا ہے۔ یہ الجبراء کی طاقت بھی ہے اور تجرید کی طاقت بھی، اور یہ صلاحیت بھی ہمارے ذہنوں میں فطری طور پر موجود ہے۔
ہندسی خاکے
ذہن کی ایک اور فطری خصوصیت کھیلنے کی خواہش اور صلاحیت ہے۔ زیادہ تر ممالیہ (دودھ پلانے والے جانداروں) میں یہ پائی جاتی ہے، جیسا کہ ہم ان کے چھوٹے بچوں کے کھیلنے کے طور طریقوں میں دیکھتے ہیں۔ اور کتے، بلی یا بندر کے بچوں کو کھیلتے ہوئے دیکھنا کتنا دلکش نظارہ ہوتا ہے، لیکن انسانوں میں ایک مزید صلاحیت ہےکہ وہ اپنے کھیلوں میں خاکے اور ترتیب بناتے ہیں۔ جب ہماری کھیلنے کی چاہت اعداد کے تصور اور خاکوں کی پسند کے ساتھ جمع ہو جاتی ہے تو ریاضی وجود میں آتی ہے۔ کیونکہ ریاضی لازما ًخاکوں کی سائنس ہے۔
ریاضی میں کھیل کے عنصر کو سمجھنا بہت اہم ہے۔ کیونکہ متعدد مرتبہ یہ سمجھایا جاتا ہے کہ ریاضی کی افادیت کیا ہے، زندگی کے مختلف مراحل میں اسکی کتنی اہمیت ہے اور ہر کسی کے پیشہ کیلئے یہ کتنی اہم ہے۔ لیکن اس نقطہ نظر میں کھیل کا عنصر نظر انداز ہو جاتا ہے۔ ریاضی ایک ایسا مضمون بن جاتا ہے کہ جس کا علم سب کیلئے لازمی ہے اور اسکے ساتھ ایک طویل ڈر کے رشتے کی بنیاد پڑتی ہے۔
قدیم ادوار سےہی بابل، یونان، چین اور ہندوستان میں ہندسی خاکوں اور جیومیٹری اشکال کے ساتھ ایک شوخ اور سحر زدہ تعلق تھا کہ جسے اعداد اور ہندسوں کے ساتھ منسلک کیا جا سکتا ہے۔ اسی سے اعداد کے مختلف اقسام مثلا پرائم نمبر(prime number)، ٹرائنگلر نمبر(triangular number)، سکوائر نمبر (square number)وغیرہ وجود میں آئے۔
اس پس منظر میں آئیے لفظ “خاکے(pattern)” کی تشریح کرتے ہیں ۔
ہم اعداد 1،2،3،4،5،۔۔۔۔۔۔۔۔۔۔۔۔ کو دو ذیلی اقسام طاق (1،3،5،7،۔۔۔۔۔۔۔۔۔۔۔) اور جفت (2،4،6،8۔۔۔۔۔۔۔۔۔۔۔) اعداد میں تقسیم کر سکتے ہیں۔
اگر ہم طاق اعداد کو جمع {رننگ ٹوٹل}کرتے جائیں تو ہمیں حاصل ہوگا: 1، 1+3=4، 1+3+5=9، 1+3+5+7=16، 1+3+5+7+9=25۔ غرض ہمیں مربع اعداد کی فہرست حاصل ہوگئ۔
اس تعجب خیز طریقے سے ہم متواتر طاق اعداد کے حاصل جمع اور مربع اعداد{اسکوائر نمبر} کے تعلق کو بتا سکتے ہیں۔
اپنی قوت میں بیک وقت دلکش اور قاطع ہونا بہت ہی دلکش ہے۔ہمیں ذیل میں دی گئی تصویر کا جائزہ لینا ہے۔ یہ خصوصیت مثلثی اعداد{ٹرائنگلر نمبر} سے قریبی تعلق رکھتی ہے۔
تسلسل 1، 3، 6، 10، 15، 21، 28، 36، 45، 55، ۔۔۔ جو کہ اعداد کے رواں حاصل جمع سے بنایا گیا ہے: 1، 1+2=3، 1+2+3=6، 1+2+3+4=10 وغیرہ۔ چونکہ ہم ان اعداد کے ساتھ مثلثی اشکال کو وابستہ کر سکتے ہیں اسلئے انہیں مثلثی اعداد یا ٹرائنگلر نمبر کہا جاتا ہے۔
ذیل میں صرف ایک سرخ مربع ہے۔ ہم اسکے اطراف تین سبز مربع جوڑ دیں تو یہ 2*2 کا مربع بناتے ہیں، اسلئے ہمارے پاس 1+3=2ضرب 2 ہے۔
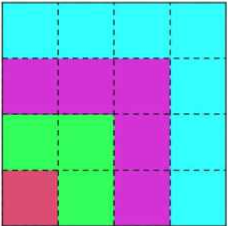
اب جامنی (بنفشی) رنگ کے پانچ مربع اور جما دیں تو آپکے پاس 3*3 کا مربع بن جائیگا؛ اسلئے 1+3+5=3ضرب 3
اب مزید سات نیلے مربع جوڑ دیں تو آپکو 4*4 کا مربع ملے گا؛ اسلئے 1+3+5+7=4 ضرب 4۔ اور اسی طرح¡
مثلثی اعداد اور مربع اعداد کو جوڑنے والی دو نمایاں خصوصیات ہیں[1،4،9،16 وغیرہ]، اور بچے انہیں آسانی سے ڈھونڈ سکتےہیں۔
۱۔ کسی بھی دو متواتر مثلثی اعداد کا مجموعہ مربع عدد ہوتا ہے۔
مثلاً 1+3=4، 3+6=9، 6+10=16، ۔۔۔
۲۔ کسی بھی مثلث عدد کو ‘8’ سے ضرب دیکر ‘1’ جمع کیاجائے تو مربع عدد حاصل ہوگا۔
مثلاً: {8*3}+1=25، {8*6}+1=49، {8*10}+1=81۔
یہ خوبصورت تعلق آخر کیوں ہے؟ غور کرنے کیلئے ایک پیارا سوال ہے۔ ہے کہ نہیں؟

یہاں ایک اور خاکہ ہے۔ کوئی تین متواتر اعداد لیجئے، مثلاً 3، 4، 5۔ درمیانی عدد کا مربع کیجئے، 16 حاصل ہوگا۔ اب دوسرے دو اعداد کو ضرب دیجئے، 3*5=15؛ غور کیجئے کہ 15-16=1؛ ان دو اعداد کا فرق 1 ہے۔ کوئی مختلف تین اعداد لیں مثلاً 7، 8، 9۔ 8 کا مربع 64 اور 9 ضرب 7 63 ہے اور 63-64=1۔ ایک اور مرتبہ فرق 1 کا ہے۔ کیا یہ تسلسل جاری رہیگا؟ جی ہاں ، اور اسے الجبراء کے استعمال سے ظاہر کرنا آسان ہوگا: لیکن ہندسوں سے کھیلتے ہوئے بچوں کو اس دریافت میں آنے والے لطف کے بارے میں ذرا سوچئے۔
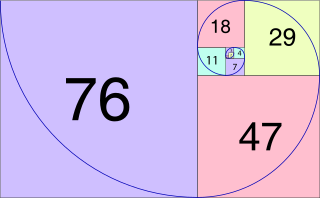
اسی سے مماثل لیکن کچھ پیچیدہ خاکہ ہمیں فیبوناکی تسلسل {فیبوناکی سیکوینس}میں ملتا ہے جو اسطرح ہے، 1، 1، 2، 3، 5، 8، 13، 21، 34، 55۔۔۔۔۔۔ یہاں پر ہر تیسرا عددپچھلے دو اعداد کا حاصل جمع ہوتا ہے۔{مثلاً 5+3=8}۔ اس تسلسل کے ساتھ حساب کو دہرائیے۔ تین اعداد 2، 3، 5 سے ہمیں حاصل ہوگا: 3 کا مربع 9، اور 2ضرب 5، 10؛ مربع کیا گیا عدد باقی دو اعداد کے حاصل ضرب سے 1 کم ہے۔ اسی طرح تین اعداد 3، 5، 8 سے ہمیں حاصل ہوگا؛ 5 کا مربع 25 اور3 ضرب 8، 24۔ اب مربع عدد حاصل ضرب سے 1 زیادہ ہے۔ اسی طرح، 5، 8، 13 سے ہمیں 8 کا مربع 64 اور 5 ضرب 13، 65 حاصل ہوگا۔ ایک بار پھر مربع عدد حاصل ضرب سے 1 کم ہے۔ یہ سلسہ اسی طرح چلتا ہے- ایک متبدل خاکہ{آلٹر نیٹینگ پیٹرن}۔
اگر ہم چار متواتر فیبوناکی اعداد کے مجموعہ کاجائزہ لیں تو ہمیں یہی تسلسل دیکھنے میں ملے گا۔ مثال کے طور پر، 1،2، 3، 5۔ خارجی دو اعداد کا حاصل ضرب 5 ہے اور اندرونی دو اعداد کا حاصل ضرب 6 ہے۔ ان دونوں میں ایک کا فرق ہے۔ اسی طرح کا ایک اور مجموعہ : 3، 5، 8، 13 ہے۔ خارجی دو اعداد کا حاصل ضرب 39 ہے اور اندرونی دو اعداد کا 40 ہے۔ ایک مرتبہ پھر فرق 1 ہے۔ اور یہاں بھی متبادل خاکہ جاری ہے۔ حیرت انگیز بات یہ ہے کہ فطرت بھی فیبوناکی اعداد کا استعمال کرتی نظر آتی ہے۔ اگر ہم مختلف پھولوں کی پنکھڑیوں کی تعداد کا اندراج کریں تو معلوم ہوگا کہ عموماً یہ ایک فیبوناکی عدد ہے۔ سورج مکھی پھول کے مرکزی حصہ اسپائرل کی شکل میں ترتیب شدہ پراگ دانوں{پولین گرینس} کا معائنہ کریں۔ یہ اسپائرل داہنی اور باہنی سمت میں بڑھ رہے ہوتے ہیں۔ آپ دیکھینگے کہ ہر سمت میں اسپائرلس کی تعداد ایک فیبوناکی عدد ہے۔ فطرت بھی ہماری طرح خاکوں کی مداح ہے۔
کئی سال قبل میں نے ” خاکے اور قوت ریاضی(“Pattern and Power of Mathematics”)” نامی ایک کتاب کا مطالعہ کیا تھا۔ یہ ایک کتاب کیلئے بہت اچھا عنوان ہے، اسلئے کہ ریاضی مضمون خاکوں ہی سے متعلق ہے اور یہی اسے غیر معمولی قوت دیتا ہے۔ لیکن- اہم ترین بات یہ ہیکہ اسی وصف کی وجہ سے ہم ریاضی پڑھنے اور سیکھنے کی طرف راغب ہوتے ہیں۔
بڑے اعداد اور چھوٹے اعداد
پہلے اعداد ہیں پھر بڑے اعداد ہیں۔ بچے فطرتاً بڑے اعداد کو پسند کرتے ہیں اور بہتوں کو یہ دریافت ہوتی ہیکہ کوئی آخری عدد نہیں ہے۔کوئی کتنا بھی بڑا عدد پیش کرے اس میں صرف 1 جمع کرنے سے اس سے بڑا عدد بن جاتا ہے۔ غرض ہندسوں کی دنیا لامتناہی ہے: اور کچھ بچے مماثل دریافت مخالف سمت میں کرتے ہیں یعنی چھوٹے اعداد کے ساتھ۔مجھے یاد آتا ہیکہ کئی سال پہلے ایک طالب علم نے بتایا تھا کہ کس طرح وہ چھوٹے سے چھوٹے کسر کی مدد سے ایک لامتناہی تسلسل بنا سکتی ہے، صرف انکو مکرر آدھا کرتے ہوئے۔ اسکےلئے یہ یقین کرنا مشکل تھا کہ اتنے چھوٹے اعداد بھی ماجاد ہیں۔ اس نے یہ حیران کن دریافت خود کی تھی اور اسکے متعلق وہ بہت پرجوش تھی۔
قدیم ہندوستانی بڑے اعداد کو پسند کرتے تھے، ایک سوال ہیکہ جو اس محبت کو ظاہر کرتا ہے۔ اگر یہاں آپ سے کہوں کہ ایک ایسا مربع عددڈھونڈیں کہ جو ایک اور مربع عدد کا دوگنا ہو تو آپ کبھی کامیاب نہیں ہونگے، کیونکہ ایسے کوئی دو عدد ہیں ہی نہیں{کیوں؟ اسکے پیچھےایک اچھی کہانی ہے لیکن یہاں ہم اسے بیان نہیں کر سکتے}۔ ہم سوال کو تھوڑابدل دیتے ہیں۔ مجھے ایک ایسا مربع عدد بتائے کہ جو کسی اور مربع عدد کے دوگنے سے بھی 1 زیادہ ہو۔ ہمیں کئی جواب ملیں گے۔مثلاً 9اور 4 مربع اعداد ہیں اور {2*4}-9=1۔ ذیل میں کچھ اور جواب ہیں۔
{2*144}-289=1
{2*4900}-9801=1
اگر ہم دوگنا کو پانچ گنا کردیں تو اسکے جواب بھی ملیں گے۔
{5*16}-81=1
{5*72*72}-{161*161}=1
اور اسی طرح۔ساتویں صدی میں برہما گپتہ نے پوچھاتھا کہ اگر ہم ‘پانچ گنا’ کو’ ۶۱ گنا’ سے تبدیل کرینگے تو کیا حل ڈھونڈا جاسکتا ہے؟ اس سوال کا سب سے چھوٹا حل بھی بہت طویل ہے لیکن برہما گپتہ نے اسے دریافت کیا۔
{1766319049*1766319049}-{61*226153980*226153980}=1۔
اس مساوات کی تصدیق کیلئے خوش آمدید۔
میں سمجھتا ہوں کہ تاریخ معنی خیز ہے: ہندوستانیوں نے تیرہ صدیوں پہلے اسطرح کے سوالات اٹھائے تھے۔ تمام انسانی تہذیبوں میں بہت طویل عرصے سے کھیل سے محبت رہی ہے اور اسے روکنے والا کوئی نہیں۔
پھر ایک عجیب واقعہ ہوا۔ جو کام ایک مشغلہ کے طور پر شروع ہوا تھا اسکے پر نکل آئے اور ایک مکمل مضمون کی طرح پرواز کرتا ہوا بہت آگے نکل گیا۔ اسکی داخلی ہم آہنگی اور بہترین تنظیم اتنے مضبوط ہیں کہ انہوں نے اشیاء کی دنیا، ذی حیات اجسام اور سرمایہ – “حقیقی دنیا” میں اپنا اطلاق ڈھونڈ لیا۔ اسطرح کی پروازیں تاریخ میں دو درجن سے زائد مرتبہ ہوچکی ہیں لیکن کوئی نہیں جانتا کہ کیوں اور کیسے واقع ہوئیں، لیکن واقع ہوئی ہیں۔ شاید یہ ہمارے لئے خدا کا تحفہ ہے۔{لیکن ہم اسکا استعمال ہمیشہ اسکی تخلیق کی منشاء کی پیروی میں نہیں کرتے؛ ریاضی کے طریقوں کا استعمال بموں کی تیاری میں، جوہری طاقت سے لیس آبدوز اور دوسرے تباہ کن آلات کی تیاری میں بھی ہوتا ہے۔}
اختتامی کلمات
ریاضی کے کئی موضاعات میں ہم خاکوں اور کھیل کے عنوان کونمایاں کرسکتے ہیں۔
* جادوئی مربع {دئے گئے 9 ہندسوں کو 3ضرب 3 کی صفوں میں یا 16 ہندسوں کو 4ضرب4 کی صفوں میں ایسے ترتیب دینا کہ قطاری مجموعہ، ستونی مجموعہ اور قطری مجموعہ ایک ہی ہوں}: اس سے نہ صرف ہندسوں کے بہتر تعلق کا اظہار ہوتا ہے بلکہ پڑھائی کے دوران بچے ممثلت{سیمیٹری} کو بھی سیکھتے ہیں۔
* کریپٹا ریتھمس(Cryptarithms){حسابی سوالات کا ایسا حل جس میں ہندسوں کو حروف سے ظاہر کیا جاتا ہے، مثال کے طور پر، ON+ON+ON = GO اوراسطرح کے سوالات کے تجزئے سے کئی سادہ مگر دلکش رموز کا پتہ لگتا ہے}۔
* 2 کی قوت والے اعدادی خاکے{متواتر 2 کی قوت والے اعداد کی بنیادی عدد لکھئے۔ آپ کیا مشاہدہ کرتے ہیں؟ اب یہی 3 کی قوت والے اعداد کے ساتھ کیجئے؛ اب کیا مشاہدہ کرتے ہیں؟}
یہ مثالیں عدد کے تصور کے اطراف بنائی گئی ہیں لیکن انکے اصول واضح طور پر جیومیٹری میں بھی استعمال ہوتے ہیں۔ رنگولی اور کولم، پیپر فولڈنگ، دائرے سے ڈیزائن وغیرہ موضوعات ہم پڑھتے ہیں۔
ان سرگرمیوں کے علاوہ، اساتذہ طلبہ اور ساتھیوں کے ساتھ گفتگو میں معاشرہ میں ریاضی کے کردار پر سوالات اٹھا سکتے ہیں۔ مثلاً ، ایسے سوالات جو تباہ کن مقاصد کیلئے ریاضی کا استعمال یا مزید عمومی سوالات جیسے ‘ریاضی کا استعمال کب مناسب ہوتا ہے؟’ یا پھر یہ کہ ‘سماج ریاضی کی سرگرمیوں کی حمایت کیوں کریگا؟’ ۔ بہر حال، اکثر آرٹسٹ اپنے آرٹ کیلئے سرپرست یا خریدار ڈھونڈلیتے ہیں لیکن ریاضی داں پیسوں کیلئے اپنے تھیرمس (theorems)فروخت نہیں کرتے۔ کیا یہ واقعہ ہے کہ پالیسی بنانے والے ریاضی کو سماج کیلئے ایک کارآمد وسیلہ مانتے ہیں اور اسلئےاس میدان کے ماہرین کو ٹیچنگ اور دوسرے کارآمد ریاضی کے ذریعہ اپنی زندگی چلانے کے مواقع فراہم کرتے ہیں؟ کارآمد یا مفید ہونے کا خیال ہمیں استعمال کی موزونیت کی طرف لے جاتا ہے۔ ایسے سوالات عام طور پر ریاضی کی درس گاہ میں موزوں نظر نہیں آتے لیکن گفتگو اور جستجو کی تہذیب کی ترویج میں انکا واضح مقام موجود ہے۔
ہمیں ایک مکمل فہرست بنانے کی کوشش نہیں کرنی چاہئے، کیونکہ یہ ممکن نہیں ہے، یہ بہت طویل ہے اور اس میں ہمیشہ اضافہ ہوتا رہتا ہے۔ بجائے اسکے، ہم اس بات پر زور دینا چاہتے ہیں کہ فن تعلیم اور نفسیاتی وجوہات کی بنا پر خاکہ اور کھیل ریاضی کی تعلیم و تدریس میں بہت اہمیت رکھتے ہیں۔
عظیم مواقع کھو جاتے ہیں جب ہم ریاضی کو ایک بوجھل اور سنجیدہ مضمون بنادیتے ہیں جو شدید مسابقتی ماحول میں صرف انتہائی باصلاحیت طلبہ کیلئےمختص ہوتا ہے۔ یہ عمل بہت سوں کو ریاضی کے تجربے سے محروم رکھتا ہے۔
———————————————
نوٹ: شائلیش شرالی، رشی ویلی اسکول میں کمیونٹی میتھ سینٹر کے سربراہ ہیں۔ انہوں نے 13-19 سال کے طلبہ کیلئے ریاضی کی کئی کتابیں تصنیف کی ہیں۔ وہ انڈر گریجویٹ سائنس میگزین’ریزوننس’ کے مدیر کی حیثیت سے بھی خدمات انجام دیتے ہیں اور ملک کی ریاضی اولمپیاڈ تحریک میں بھی بہت سرگرم ہیں۔ ان سے رابطہ کیلئے ای میل درج ذیل ہے۔
[email protected]
مترجم : سید نثار احمد ، لکچرر دکن انجنیرنگ کالج
بشکریہ :لرننگ کرو (ریاضی پر خصوصی شمارہ)، عظیم پریم جی یونیورسٹی، بنگلور